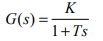Margen de fase y Ganancia

Margen de fase y Ganancia Para sistemas de fase mínima en bucle abierto, si la respuesta en frecuencia de la función de transferencia G(s)·H(s) presenta frecuencias en las que la ganancia es positiva a la vez que la fase tiene un valor inferior a -180º el sistema realimentado negativamente, M(s), será inestable. • Margen de fase: Es el ángulo (en grados) que habría que restarle a la fase de G(s)·H(s) para volver inestable a M(s). Sobre las representaciones gráficas de la respuesta en frecuencia de G(s)·H(s), es el ángulo que le falta a la fase para llegar a -180º cuando la ganancia es 1 (0 dB). (Si la ganancia es siempre inferior a 0 dB el margen de fase será infinito) • Margen de ganancia : Es el valor por el que habría que multiplicar (o los dB que habría que sumar a) la ganancia de G(s)·H(s), para que M(s) se vuelva inestable. Es decir, para que cuando la fase sea -180º la ganancia fuese 1 (0...