sistemas continuos de primer orden y segundo orden

Se denomina orden de un sistema al grado de su polinomio característico. Consecuentemente el orden de un sistema coincide con el número de polos de éste y con el orden de la ecuación diferencial que lo modela. Los sistemas más sencillos y representativos son los de 1er y 2º orden. El análisis de la respuesta temporal de los sistemas se hace a partir de su respuesta a ciertas entradas, en particular al escalón unitario u(t). 

Un sistema de 1er orden tiene una función de transferencia de la forma: 

La respuesta de este sistema ante una entrada escalón unitario tiene por expresión: 

La representación gráfica de esta expresión puede verse en la siguiente grafica.


Los parámetros característicos que aparecen representados en la figura anterior son:

- K: La ganancia estática se define como el valor final ante entrada escalón unitario.

- T: Constante de tiempo (es el tiempo en el que se alcanza el 63% del valor final).

- ts= 3T: Tiempo de establecimiento (es el tiempo que tarda la respuesta en entrar y

permanecer en la zona del ±5% en torno a su valor de equilibrio). 

Los sistemas de 2º orden tienen una función de transferencia de la forma: 


Pudiendo considerar los siguientes parámetros: 

Los dos polos de este sistema pueden ser reales o complejos conjugados, dependiendo del valor que tome el coeficiente de amortiguamiento.

Para el caso de tener polos complejos conjugados estos serán de la forma: 

Si σ es positivo el sistema será estable. Si ξ es mayor que la unidad, los polos serán reales y el sistema no presentará oscilaciones. Por el contrario si ξ es menor que la unidad, los polos serán complejos y el sistema oscilará. 

ξ < 0 INESTABLE
 ξ > 1 SOBREAMORTIGUADO
 ξ = 1 CRITICAMENTE AMORTIGUADO
 0 < ξ < 1 SUBAMORTIGUADO 

La respuesta de un sistema de segundo orden subamortiguado, ante entrada escalón unitario, queda representada en la figura 2 donde aparecen una serie de parámetros característicos cuya denominación, significado y valor se dan a continuación. 

Pendiente en el origen. 
Tiempo de establecimiento
Tiempo de subida.
Tiempo de pico. 
Sobre oscilación.












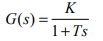
Comentarios

Publicar un comentario

Entradas populares de este blog

regla de masón

Imagen
 Definiciones: Trayecto: Recorrido directo entre dos líneas en el sentido de las flechas, pasando solo una vez por cada bloque o línea.  Lazo: Trayecto que se cierra sobre si mismo, partiendo de una línea y regresando a la misma línea. Lazo adjunto: son aquellos lazos que comparten algún tramo del diagrama. Lazo NO adjunto: Aquellos lazos que no poseen ninguna línea en común; esto es, no se tocan. Ganancia del trayecto: Producto de las transmitancias de los bloques de un trayecto, tomando en cuenta los signos de los sumadores. Ganancia de lazo: Producto de las transmitancias de los bloques de un lazo, tomando en cuenta los signos de los sumadores. ecuaciones: La regla de Masón permite encontrar la transmitancia G entre  cualquier par de variables (líneas) de un sistema. Donde: Ti = Ganancia del i-ésimo trayecto de los n posibles entre las  dos líneas. Δ = Determinante del diagrama = 1 – (suma de todas las ganancias de lazo distintos posibles) +  (suma de los pro...
Leer más

Respuesta al impulso

Imagen
 ¿Qué es una respuesta de impulso? Una respuesta de impulso (IR) se puede definir como la respuesta en el dominio del tiempo (tiempo vs. amplitud) del sistema que estamos analizando bajo un estímulo sonoro de corta duración. Esto quiere decir que nos va a mostrar información tanto de amplitud como de tiempo, nos va a mostrar qué sucede en el sistema a analizar durante el paso del tiempo. Seguro que muchos, cuando entráis en un espacio donde vais a realizar una sonorización, dais una palmada para escuchar cómo se comporta el sonido en ese espacio. Pues bien, eso es un impulso (la palmada) y la respuesta al impulso (cómo se comporta la sala con ese estímulo). Una palmada o una explosión de un globo podría ser un impulso, y por tanto lo podríamos utilizar para excitar el sistema que queremos medir. El sistema a analizar puede ser desde un micrófono o un altavoz, a un dispositivo electrónico como un ecualizador. O incluso una habitación, o cómo se comporta una habitación con una determ...
Leer más

sistemas discretos de primer orden y segundo orden

Imagen
 sistemas de discretos de primer orden Supóngase un sistema discreto de primer orden, cuya función de transferencia sea Al estimular el sistema con un paso unitario  µ ( k ), con condiciones iniciales nulas, la respuesta  y ( k ) puede calcularse como sigue: La expresión (4.4) muestra que la respuesta del sistema depender 'a del valor de  a . Este hecho se constata en la figura 4.1, que muestra las gráficas de  y  ( k ) para distintos valores de  a  .Al cambiar el valor de  a  también cambia el valor de el ´único polo de la funcione transferencia (4.3), que es − a . Para cualquier valor real positivo de  a  el polo es un real negativo  −  a , y viceversa. Cuando el polo es negativo, la respuesta del sistema es de signo alternante por el contrario, si el polo es positivo la respuesta siempre será del mismo signo. Por otra parte, si el valor absoluto de  a  es mayor que 1, el ...
Leer más