Respuesta al impulso
¿Qué es una respuesta de impulso?
Una respuesta de impulso (IR) se puede definir como la respuesta en el dominio del tiempo (tiempo vs. amplitud) del sistema que estamos analizando bajo un estímulo sonoro de corta duración.
Esto quiere decir que nos va a mostrar información tanto de amplitud como de tiempo, nos va a mostrar qué sucede en el sistema a analizar durante el paso del tiempo.
Seguro que muchos, cuando entráis en un espacio donde vais a realizar una sonorización, dais una palmada para escuchar cómo se comporta el sonido en ese espacio. Pues bien, eso es un impulso (la palmada) y la respuesta al impulso (cómo se comporta la sala con ese estímulo).
Una palmada o una explosión de un globo podría ser un impulso, y por tanto lo podríamos utilizar para excitar el sistema que queremos medir.
El sistema a analizar puede ser desde un micrófono o un altavoz, a un dispositivo electrónico como un ecualizador. O incluso una habitación, o cómo se comporta una habitación con una determinada fuente sonora en ella.
Si hablamos de análisis acústico, podemos entender la respuesta de impulso como la “firma acústica” del sistema que analizamos, en el sentido de que cada elemento que midamos tendrá una respuesta de impulso distinta.
Pero… ¿qué información podemos obtener de un impulso si no se tiene en cuenta la frecuencia y tiene tan poca duración?
Aquí entra en juego la transformada de Fourier, que nos permite relacionar el dominio frecuencial con el dominio del tiempo.
El sonido de la fuente de la imagen de arriba (la explosión de un globo, es decir, un impulso) va a llegar a la posición de medición por diferentes caminos (y deferentes tiempos), tanto directos como reflejados. Vemos en rojo el camino directo, y en azul, verde y gris las diferentes reflexiones. . El sistema de medición nos mostrará la respuesta de impulso en una gráfica de tiempo y amplitud.
Una respuesta de impulso pertenece al dominio temporal, pero se puede convertir al dominio frecuencial mediante la transformada de Fourier (y viceversa).
A partir de la Respuesta de Impulso se obtiene gran cantidad de información acerca de un sistema acústico, incluyendo los tiempos de llegada y contenido en frecuencia tanto del sonido directo como de las reflexiones.
También se puede obtener información del tiempo de reverberación, la relación señal-ruido e información sobre la inteligibilidad y la respuesta en frecuencia general.
Elementos de la respuesta de impulso.
Una respuesta de impulso acústica se crea emitiendo sonido desde una fuente. El sonido directo llegará primero y con más nivel al punto de medición.
El sonido reflejado llegará más tarde por los múltiples rebotes, perdiendo energía debido a la absorción de aire y de las superficie con las que se encuentre a lo largo del camino, por lo que tendrá niveles cada vez más bajos.
La parte que nos interesa analizar abarca unos pocos segundos o incluso menos de un segundo en habitaciones pequeñas una acústica muy absorbente.
La llegada a nuestro sistema de medición del sonido directo y probablemente del sonido reflejado se podrá distinguir claramente en una gráfica de respuesta de impulso.
El sonido directo se verá en la gráfica de tiempo vs amplitud como una gran señal y las reflexiones posteriores llegarán después con menor nivel.
El pico inicial nos indica la llegada del sonido directo, y los siguientes picos más pequeños indican la llegada de diferentes reflexiones, más tarde, al punto de medición.
Aunque dos habitaciones distintas van a tener respuestas de impulso diferentes, hay ciertos componentes comunes que probablemente podremos identificar cuando visualicemos las respuestas de impulso.
Estos elementos comunes son los siguientes:
- Llegada de la señal directa.
- Primera reverberación generada y su pendiente de caída.
- Primeras reflexiones.
- Ruido de fondo.
Hasta ahora habíamos visto la gráfica de la respuesta de impulso en modo lineal (tiempo en el eje horizontal y amplitud en el eje vertical). Pero si la visualizamos la respuesta de impulso en modo logarítmico tenemos mucha más información a simple vista.
La respuesta de impulso en modo logarítmico nos muestra la amplitud en decibelios y en el eje horizontal el tiempo, normalmente en milisegundos. Otra forma de visualización, en la que no voy a profundizar, pero que conviene saber que existe, es la llamada ETC (Envelope Time Curve), útil por ejemplo para sincronizarse con señales de baja frecuencia.
Tiempo de propagación:
Es el tiempo que tarda el sonido directo de la fuente en llegar a la posición de medición.
Dentro de este tiempo de propagación se incluye la latencia que pueda producir cualquier elemento digital que esté conectado a nuestra cadena de audio y el tiempo que tarda el sonido en viajar por el aire desde la fuente al punto de medición.
Llegada del sonido directo:
Dado que la distancia más corta entre dos puntos es siempre la línea más recta, lo primero que esperamos ver cuando analizamos una respuesta de impulso es la llegada del sonido directo de la fuente de sonido que estamos utilizando para estimular el sistema. Con este tiempo de llegada es con el que se sincroniza nuestro analizador FFT cuando buscamos el delay en la función de transferencia.
Primeras reflexiones:
Después de la llegada del sonido directo, las siguientes características más destacadas que tendemos a ver llegar son las primeras reflexiones. Estas primeras reflexiones son normalmente de primer orden. Esto quiere decir que el sonido sólo ha rebotado en una superficie antes de llegar al punto de medición.
Primera caída y reverberación:
Tras la llegada del sonido directo y las reflexiones de orden más bajo, el sonido en un espacio reverberante continuará rebotando por la habitación durante un tiempo, creando reflexiones cada vez de mayor orden y menor energía.
En cualquier posición de escucha, parte de esta energía reflejada se combinará de forma constructiva durante un relativamente corto período de tiempo, lo que dará como resultado una acumulación de sonido reverberante.
Está estandarizado que la caída de 10dB después de la llegada del sonido directo sea considerada la primera caída o early decay.
La caída de la reverberación se mide normalmente desde 5dB por debajo del nivel de sonido directo hasta el punto en el que el sonido cae 35dB (TR30). En el caso de que las condiciones de la medida no permitan tener una caída de 30dB (35-5), se puede realizar una medida con una caída de 20dB (RT20). Después, el software será capaz de calcular el RT60.
Ruido de fondo:
En la práctica siempre vamos a llegar a un punto en que nuestra medición del impulso no se pueda distinguir del ruido de fondo al quedar por debajo de este. Cuanto más alto sea el ruido de fondo, a mayor nivel tendremos que emitir nuestra señal de impulso para conseguir una buena respuesta de medición.
La función Impulso Unitario
La función impulso unitario δ(t), también conocida como Delta de Dirac, tiene un papel fundamental en el análisis de señales. La misma está definida de la siguiente manera:
Esta señal de puede ver como un pulso rectangular de área unidad, ancho ε y altura 1/ε
Como se puede ver en la Figura anterior, la función impulso unitario es una función par, es decir:
La función impulso unitario δ(t) no es una función en el sentido ordinario como se define una función. Una función ordinaria viene especificada para todos sus valores de tiempo t. La función impulso unitario es cero para todo valor de t, excepto en t=0, y este es el único punto interesante de su dominio, y sin embargo aquí su valor es indefinido. Más útil es definir la función impulso unitario δ(t) como una función generalizada. Una función generalizada se define por sus efectos sobre otras funciones, en vez de ser definida por los valores que asume en su dominio.
En este caso, la función impulso unitario δ(t) se define sobre todo por su propiedad de muestreo y por su propiedad de selección.
Otra manera de decirlo es que la función impulso unitario δ(t) está mejor definida por sus aplicaciones que por los valores que asume en su dominio.
Supongamos la multiplicación entre la función δ(t) y una función cualquiera Φ(t) continua en t=0, donde la función tiene una magnitud Φ(0) en ese punto. Se obtiene que:
Este resultado es de gran importancia y se va a aplicar en la siguiente propiedad. Además, se puede generalizar para una función impulso unitario desplazado en t=T:
Integrando el resultado de la propiedad anterior y utilizando la definición del impulso unitario dado al principio, obtenemos que:
La anterior es una de las propiedades más importantes en el análisis de señales y sistemas. Este resultado se puede generalizar como:
Se puede demostrar que:
Lo que implica que:
Una aplicación de gran importancia en cuanto a la función impulso unitario, es que hace posible la existencia de la derivada de la función escalón unitario en t=0, lo cual no es posible en el sentido de una función ordinaria, pero si en el sentido de una función generalizada. Para esto, integramos el producto de la función Φ(t) definida anteriormente y du(t)/dt:}
Este resultado demuestra que du(t)/dt satisface la propiedad de selección de δ(t). Es decir, en términos de una función generalizada:
En consecuencia:
A continuación pasamos a estudiar el caso tiempo discreto.
Impulso unidad delta.
Se trata de una de las señales discretas más simples, la señal impulso unitario discreto, la cual se define como:
De hecho, la señal impulso unitario discreto es la base de la representación de las señales discretas, cualquier señal discreta se puede obtener como combinación lineal de deltas desplazadas. El ejemplo más relevante es el escalón unidad o escalón unitario.
La señal escalón unitario se define como:
El escalón unitario es la suma de un tren de impulsos:
De esta manera, complementado el caso de tiempo continuo, el impulso unidad se puede expresar como:
También se puede expresar el escalón unitario como:
Es interesante constatar que en el caso del impulso unidad también se cumple la propiedad de muestreo:
En general, cualquier señal discreta x[n] puede ser representada como una combinación lineal de deltas desplazadas. En general se cumple que:















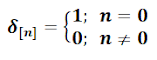










Comentarios
Publicar un comentario