clasificación de los modelos matemáticos

 Clasificación de los modelos Matemáticos

Un modelo Matemático en términos sencillos es un grupo de ecuaciones o inecuaciones que representan una realidad. El ingrediente principal en un modelo matemático, como es de esperarse, es la variable. Las variables, son la representación de los diferentes posibilidades

de un conjunto de datos y estos datos en su origen pueden ser de tipo Determinísticos o estocásticos.

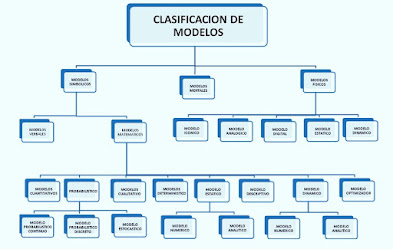
Figura II.11 Clasificación de los modelos matemáticos

Determinísticos

Los modelos determinísticos son los que hacen predicciones definidas de cantidades, dentro de cualquier distribución de probabilidades, también se les puede definir como aquellos que se aplican a problemas en los que hay un solo estado de la naturaleza, y dónde variables, limitaciones y alternativas son, después de que se aceptan los supuestos, conocidos, definibles, finitos y predecibles con confidencia estadística. Algunos modelos, herramientas o técnicas determinísticos son: programación lineal, análisis de Markov, costo/beneficio, etc. En otras palabras, un modelo determinístico se construye para una condición de certeza supuesta, y el modelo asume que solo hay un resultado posible (el cual es conocido) para cada acción o curso alternativo.

Los modelos determinísticos se clasifican a su vez en:

• Lineales

Lineales.- Llamamos modelos lineales a aquellas situaciones que después de haber sido analizadas matemáticamente, se representan por medio de una función lineal. En algunos casos nuestro modelo coincide precisamente con una recta, en otros casos, a pesar de que las variables que nos interesan no pertenecen todas a la misma línea, es posible encontrar una función lineal que mejor se aproxime a nuestro problema, ayudándonos a obtener información valiosa. Nuestro modelo lineal se puede determinar de manera gráfica o bien, por medio de una ecuación. Existen ocasiones en que a una de nuestras variables le pedimos que cumpla varias condiciones a la vez, entonces surge un conjunto de ecuaciones donde el punto de intersección de dichas ecuaciones representa la solución de nuestro problema.

Dentro de la categoría de modelos lineales tenemos los siguientes: o Modelo de Redes.

o Programación lineal.

• Modelo de Redes.- la familia de redes de los problemas de optimización incluye los siguientes prototipos de modelos: Problemas de asignación, camino crítico, flujo máximo, camino más corto, transporte y costo mínimo de flujos. Los problemas son establecidos fácilmente mediante el uso de arcos de redes y de los nodos.

Los modelos de redes son aplicables a una extensa variedad de problemas de decisión, los cuales pueden ser modelados como:

• Problemas de optimización de redes que pueden ser eficiente y efectivamente resueltos.

• Algunos de estos problemas de decisión son realmente problemas físicos, tales como el transporte o flujo de bienes materiales.

• Sin embargo, muchos problemas de redes son más que una representación abstracta de procesos o actividades, tales como el camino crítico en las actividades entre las redes de un proyecto gerencial.

• Juegan un papel importante en la gerencia logística y en la cadena de insumos para reducir costos y mejorar servicios. Por lo tanto, el objetivo es encontrar la manera más efectiva en término de costos para transportar bienes.

• Programación lineal.- es un procedimiento o algoritmo matemático mediante el cual se resuelve un problema indeterminado, formulado a través de ecuaciones lineales, optimizando la función objetivo, también lineal.

Consiste en optimizar (minimizar o maximizar) una función lineal, que denominaremos función objetivo, de tal forma que las variables de dicha función estén sujetas a una serie de restricciones que expresamos mediante un sistema de inecuaciones lineales.

La Programación Lineal (PL) es un procedimiento matemático para determinar la asignación óptima de recursos escasos. La PL es un procedimiento que encuentra su aplicación práctica en casi todas las facetas de los negocios, desde la publicidad hasta la planificación de la producción. Problemas de transporte, distribución, y planificación global de la producción son los objetos más comunes del análisis de PL.

Aplicabilidad de la Programación Lineal

Aplicación de la programación lineal

La Programación Lineal permite resolver problemas de:

• Mezclas

• Nutrición de animales

• Distribución de factorías

• Afectación de personal a distintos puestos de trabajo

• Almacenaje

• Planes de producción

• Problemas de circulación

• Planes de optimización de semáforos

• Estudios de comunicaciones internas

No lineales.- Los modelos no lineales se caracteriza por ser muy diversos, de tal manera que incluso el caos forma una parte pequeña de los modelos no lineales; esto es, cuando el modelo no lineal va a predecir que el resultado no es predecible. Sin embargo, su interés se centra en predecir los resultados de la manera más exacta posible.

Dentro de la categoría de modelos no lineales tenemos los siguientes: o Programación Dinámica

o Programación Heurística o Programación no lineal

• Programación Dinámica.- La Programación Dinámica es un método de solución de problemas que permite descomponer un modelo matemático muy grande, en problemas más pequeños de fácil resolución, que al resolver cada uno de ellos se obtiene la solución apropiada al problema mayor del cual fueron generados los más pequeños. La programación dinámica se apoya como estrategia de solución en “divide y vencerás”. En sí, la programación dinámica, no tiene una técnica específica que se aplique a todos los problemas para resolverlos como es el caso de la programación lineal. Más bien, es un método de resolución de problemas, que aunque mantiene algunas características comunes entre unos y otros, cada aplicación requiere un grado de práctica, creatividad y conocimientos para lograr dividir el problema grande en muchos pequeños lógicos y que se encuentren relacionados entre sí.

La Programación dinámica se puede aplicara para resolver problemas como:

o Problema de la mochila (Snapsack Problem) o Problema de la diligencia (Stagecoach Problem)

• Programación Heurística.- Está basado en el modelo de comportamiento humano y su estilo para resolver problemas complejos, además, implica una forma de modelizar el problema en lo que respecta a la representación de su estructura, estrategias de búsqueda y métodos de resolución. Existen diversos tipos de programas que incluyen algoritmos heurísticos. Varios de ellos son capaces de aprender de su experiencia.

Aplicabilidad de la Programación Heurística

La programación heurística según varios autores es que el método heurístico forma parte vital, pero despreciada; del conjunto de herramientas del analista de investigación operacional. No se sugiere, sin embargo que todo problema sea resuelto por programación heurística. De hecho, la programación heurística se debe considerar únicamente si es obvio que los otros métodos fallarán. El punto es que este tipo de programación debe ser utilizada solamente cuando las técnicas exactas no están disponibles y/o no son económicas.

Los dos usos principales del enfoque de programación heurística son:

• Para resolver problemas de tal magnitud, que métodos más exactos y elegantes no pueden ser empleados.

• Para obtener un valor de iniciación aceptable, si no óptimo para los procedimientos más elegantes.

Ejemplos:

o Utilizando solo dos cubos sin marcas, uno de 6 litros y otro para 8 litros de capacidad; llenar un cubo con cuatro litros de agua.

o Determinar la mejor asignación de 50 puestos de trabajo, con cada uno de los 30 operarios de una empresa.

• Programación no Lineal.- es el proceso de resolución de un sistema de igualdades y desigualdades sujetas a un conjunto de restricciones sobre un conjunto de variables reales desconocidas, con una función objetivo a maximizar, cuando alguna de las restricciones o la función objetivo no son lineales. Cuando el conjunto de restricciones, la función objetivo, o ambos, son no lineales, se dice que se trata de un problema de programación no lineal (PPNL).

Aplicabilidad de la Programación no Lineal

Podemos resolver con programación no lineal problemas:

• Bidimensionales

• Tridimensionales

• Optimización

• Estimación de estado en sistemas eléctricos

• Reparto optimo de carga

• Ejemplos geométricos

• Ejemplos mecánicos

Aleatorios o Estocásticos. Los modelos estocásticos contienen elementos aleatorios distribuidos dentro del modelo; de tal manera que predicen el valor previsto o una cantidad en términos de probabilidad de ocurrencia; también se les puede definir como aquellos modelos cuantitativos en los que hay más de un estado de la naturaleza y donde cada estado debe estimarse o definirse para permitir el cálculo de los resultados condicionales de cada alternativa de decisión en cada estado; cuando riesgo e incertidumbre están implicados en el problema de decisión, se emplean los modelos probabilísticas cuantitativos.

Dentro de la categoría de aleatorios o estocásticos tenemos los siguientes: o Simulación

o Teoría de Juegos o Procesos de Markov o Arboles de decisión

• Simulación.- Simulación es el proceso de diseñar y desarrollar un modelo computarizado de un sistema o proceso y conducir experimentos con este modelo con el propósito de entender el comportamiento del sistema o evaluar varias estrategias con las cuales se puede operar el sistema. Es imitar una situación del mundo real en forma matemática. La simulación constituye una técnica económica que nos permite ofrecer varios escenarios posibles de una

situación y nos permite equivocarnos sin provocar efectos sobre el mundo real (por ejemplo un simulador de vuelo o conducción).

Aplicabilidad de la Simulación

La simulación surge en tipos diferentes de problemas:

o Problemas que involucrarán una clase de proceso estocástico: Demanda por un articulo, tiempo de espera antes de empezar una producción, etc.

o Ciertos problemas matemáticos completamente determinísticos que no pueden resolverse fácilmente por métodos analíticos o determinísticos; sin embargo, es posible obtener soluciones aproximadas a estos simulando un proceso estocástico cuyos momentos, función de densidad o de distribución satisfacen las relaciones funcionales o los requisitos del problema determinístico: ejemplo: Ecuaciones diferenciales complejas.

o Cuando se está estudiando un sistema por medio de investigación de operaciones, es necesario usar la simulación en aquellas etapas que estén ocasionando dificultades. o La simulación además puede realizarse para verificar soluciones analíticas.

o También permite estudiar los sistemas dinámicos, ya sea en tiempo real, comprimido o expandido.

• Teoría de Juegos.- La teoría de juegos es un área de la matemática aplicada que utiliza modelos para estudiar interacciones en estructuras formalizadas de incentivos (los llamados juegos) y llevar a cabo procesos de decisión. Sus investigadores estudian las estrategias óptimas así como el comportamiento previsto y observado de individuos en juegos. Tipos de interacción aparentemente distintos pueden, en realidad, presentar estructuras de incentivos similares y, por lo tanto, se puede representar mil veces conjuntamente un mismo juego.

Aplicabilidad de la teoría de juegos

Desarrollada en sus comienzos como una herramienta para entender el comportamiento de la economía, la teoría de juegos se usa actualmente en muchos campos, desde la biología a la filosofía.

Desde los setenta, la teoría de juegos se ha aplicado a la conducta animal, incluyendo el desarrollo de las especies por la selección natural. A raíz de juegos como el dilema del prisionero, en los que el egoísmo generalizado perjudica a los jugadores, la teoría de juegos se ha usado en economía, ciencias políticas, ética y filosofía. Finalmente, ha atraído también la atención de los investigadores en informática, usándose en inteligencia artificial y cibernética. Los analistas de juegos utilizan asiduamente otras áreas de la matemática, en particular las probabilidades, las estadísticas y la programación lineal, en conjunto con la teoría de juegos.

• Procesos de Márkov.- Una cadena de Márkov, recibe su nombre del matemático ruso Andrei Andreevitch Márkov (1856-1922), es una serie de eventos, en la cual la probabilidad de que ocurra un evento depende del evento inmediato anterior. En efecto, las cadenas de este tipo tienen memoria. "Recuerdan" el último evento y esto condiciona las posibilidades de los eventos futuros. Esta dependencia del evento anterior distingue a las cadenas de Márkov de las series de eventos independientes, como tirar una moneda al aire o un dado. En los negocios, las cadenas de Márkov se han utilizado para analizar los patrones de compra de los deudores morosos, para planear las necesidades de personal y para analizar el reemplazo de equipo.

Aplicabilidad de los Procesos de Márkov

o Los procesos de Markov aparecen ampliamente en la física, en particular la mecánica estadística, siempre que las probabilidades se utilizan para representar detalles desconocidos del sistema.

o Teoría de colas y en estadística.

o Estado efectivo de estimación y reconocimiento de patrones. o Reconocimiento de voz

o Bioinformática, por ejemplo para la codificación de región o de predicción de genes. o Comportamiento de navegación web de los usuarios.

o Generación de secuencias de números aleatorios. o Modelos biológicos.

o Geoestadística. o Juegos de azar.

• Árboles de decisión.- El árbol de decisión es un diagrama que representan en forma secuencial condiciones y acciones, muestra qué condiciones se consideran en primer lugar, en segundo lugar y así sucesivamente. Este método permite mostrar la relación que existe entre cada condición y el grupo de acciones permisibles asociado con ella, además, modela funciones discretas, en las que el objetivo es determinar el valor combinado de un conjunto de variables, y basándose en el valor de cada una de ellas, determinar la acción a ser tomada. Los árboles de decisión son normalmente construidos a partir de la descripción de la narrativa de un problema. Ellos proveen una visión gráfica de la toma de decisión necesaria, especifican las variables que son evaluadas, qué acciones deben ser tomadas y el orden en la cual la toma de decisión será efectuada. Cada vez que se ejecuta un árbol de decisión, solo un camino será seguido dependiendo del valor actual de la variable evaluada.