DINAMICA DE SISTEMAS

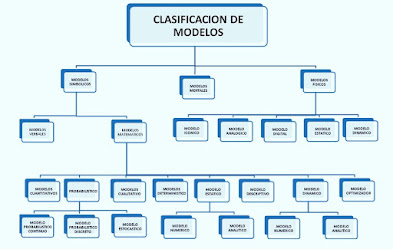
Como se menciono en la entradas anteriores un sistema no es mas que un conjunto de componentes que se utilizan para alcanzar un objetivo especifico, sin embargo al momento de hablar de sistemas físicos se requieren los modelados o modelos matemáticos , un m odelo matemático es cualquier diseño o sistema que parte de una predicción de su funcionamiento antes antes de que dicho sistema pueda diseñarse detalladamente o construirse físicamente.  Un sistema físico por ende requiere de modelos matemáticos pues como se menciona que es un sistema  físico  este requiere hacer uso de leyes y ecuaciones para comprender y predecir su funcionamiento un claro ejemplo seria en los sistema de traslación y r otación pues ambos se basan en la segunda ley de Newton el cual es un modelo matemático, dichos modelos matemáticos son interpretados como ecuaciones diferenciales. Puede haber distintos sistemas físicos los cuales se pueden clasificar de la siguiente manera: Circuitos Eléctricos Sistemas trasl

La  analogía se ha utilizado durante muchos años, especialmente cuando aún no existía la forma de utilizar computadoras digitales para la simulación de procesos con el fin de obtener circuitos eléctricos que permitan simular el comportamiento del sistema real. En concreto, buscamos un circuito eléctrico cuyas ecuaciones tengan la misma forma que las ecuaciones que definen el sistema a analizar.  Las expresiones analógicas para el circuito eléctrico se obtienen a partir de las ecuaciones que definen el comportamiento del sistema utilizando las variables analógicas, y se representa este circuito. Esto permitió, por ejemplo, construir un circuito eléctrico análogo a un sistema mecánico dado y poder simular el comportamiento del sistema mecánico a través del circuito eléctrico sin tener que producir los componentes mecánicos para cada una de las posibles condiciones de simulación. La analogía permite establecer relaciones entre sistemas de cualquier tipo, se pueden destacar como las de may

L inealización de modelos no lineales La  linealidad y no linealidad de un modelo matemático se puede referir bien a las variables o a los parámetros.  Se dice que una ecuación es lineal en variables si su representación de "y" frente a "x" es una línea.  Una ecuación se considera lineal en los parámetros si "x" se considera una constante, la dependencia de "y" de los parámetros es una combinación de sumas y líneas rectas.   La no linealidad es todo lo contrario de lo que se dijo. El modelo matemático es no lineal cuando las ecuaciones diferenciales que lo componen contienen términos que son funciones no lineales de las variables dependientes o de estado, de control o de salida. Incluso para procesos aparentemente simples, el modelo suele ser no lineal. L a linealización del modelo se efectuará en torno al régimen nominal de operación, por lo que las soluciones que se obtengan sólo serán válidas para estudiar el comportamiento dinámico del proces

 Los sistemas LTI son aquellos que cumplen con las propiedades de linealidad e invarianza en el tiempo. De allí las siglas que provienen del inglés “Linear and Time-Invariant”. Su importancia radica en que facilitan enormemente el estudio y análisis de sistemas complejos que puedan ser representados mediante un modelo matemático que cumpla con estas dos condiciones. Incluso cuando se posee poca información sobre un sistema, un modelo LTI del mismo permite predecir rápidamente como se va a comportar, cuál será la salida para una determinada entrada de prueba, que puede ser un impulso (movimiento súbito que desaparece de inmediato), un escalón (movimiento súbito que se mantiene constante), o una rampa (movimiento que crece o decrece de forma lineal). Un sistema lineal, en tiempo continuo o discreto, es aquel que posee la importante propiedad de la superposición: si una entrada consiste en la suma ponderada de varias señales, entonces la salida es simplemente la superposición (es decir, l

 Clasificación de los modelos Matemáticos Un modelo Matemático en términos sencillos es un grupo de ecuaciones o inecuaciones que representan una realidad. El ingrediente principal en un modelo matemático, como es de esperarse, es la variable. Las variables, son la representación de los diferentes posibilidades de un conjunto de datos y estos datos en su origen pueden ser de tipo Determinísticos o estocásticos. Figura II.11 Clasificación de los modelos matemáticos Determinísticos Los modelos determinísticos son los que hacen predicciones definidas de cantidades, dentro de cualquier distribución de probabilidades, también se les puede definir como aquellos que se aplican a problemas en los que hay un solo estado de la naturaleza, y dónde variables, limitaciones y alternativas son, después de que se aceptan los supuestos, conocidos, definibles, finitos y predecibles con confidencia estadística. Algunos modelos, herramientas o técnicas determinísticos son: programación lineal, análisis de

 Para este tema consideramos que primero hay que tener un concepto que nos ayude a ponernos en concepto: Un modelo matemático es una representación simplificada, a través de ecuaciones, funciones o fórmulas matemáticas, de un fenómeno o de la relación entre dos o más variables. La rama de las matemáticas que se encarga de estudiar las cualidades y estructura de los modelos es la llamada “teoría de los modelos”. ¿Para qué sirve un modelo matemático? Los modelos matemáticos son utilizados para analizar la relación entre dos o más variables. Pueden ser utilizados para entender fenómenos naturales, sociales, físicos, etc. Dependiendo del objetivo buscado y del diseño del mismo modelo pueden servir para predecir el valor de las variables en el futuro, hacer hipótesis, evaluar los efectos de una determinada política o actividad, entre otros objetivos. Aunque parezca un concepto teórico, en realidad hay muchos aspectos de la vida cotidiana regidos por modelos matemáticos. Lo que ocurre es que

señales una señal se puede definir como una portadora física de información. por ejemplo, las señales de audio son variaciones en la presión de aire llevando consigo un mensaje a nuestros oídos y las señales visuales son ondas de luz que llevan información a nuestros ojos. desde un punto de vista mas matemático, las señales se representan por una función de una o mas variables. Modelos  Un modelo de un sistema es básicamente una herramienta que permite responder interrogantes sobre este último sin tener que recurrir a la experimentación sobre el mismo. Es una representación siempre simplificada de la realidad (si el sistema físico existe) o es un prototipo conceptual (proyecto del sist. Físico).  Modelos matemáticos:  Son expresiones matemáticas que describen las relaciones existentes entre las magnitudes caracterizantes del sistema. Pueden ser sistemas de ecuaciones, inecuaciones, expresiones lógico-matemáticas. Todas estas formas vinculan variables matemáticas representativas de las

 Los sistemas dinámicos permiten obtener o predecir valores de una determinada magnitud para dar respuesta a problemas o necesidades del mundo real (físicas, económicas, médicas…). Un sistema es un ente u objeto que está compuesto de diferentes componentes o partes que se interrelacionan de alguna manera entre sí (con todos los demás o con alguno de ellos). Según la teoría de sistemas, todos los entes u objetos son un sistema en sí mismos o son componentes de otro sistema de mayor nivel. Los sistemas dinámicos son aquellos en los que su comportamiento cambia o evoluciona con el paso del tiempo y estas modificaciones o transformaciones de su estado pueden ser analizadas o modeladas mediante modelos matemáticos. La metodología que permite estudiar y describir cómo afecta el entorno y la iteración entre los componentes y partes que conforman el sistema a lo largo del tiempo al comportamiento o estado del sistema se denomina «dinámica de sistemas». Claves de los sistemas dinámicos Matemáti

 Creo que para dar un buen inicio a este nuevo blog que tratara de la materia dinámica de sistemas lo primero que hay que hacer es un resumen del concepto de este. La Dinámica de Sistemas es una herramienta de construcción de modelos de simulación (por ejemplo con Vensim ) radicalmente diferente al de otras técnicas aplicadas el estudio de sistemas socioeconómicos, como la econometría. Las técnicas econométricas, basadas en un enfoque conductista, emplean los datos empíricos como base de los cálculos estadísticos para determinar el sentido y la correlación existente entre los diferentes factores. La evolución del sistema analizado se realiza sobre la base de los datos históricos de las variables denominadas independientes, y se aplica la estadística para determinar los parámetros del sistema de ecuaciones que las relacionan con las otras denominadas dependientes. Estas técnicas pretenden determinar el comportamiento del sistema sin entrar en el conocimiento de sus mecanismos internos.